The Binding Affinity Calculator (BAC) application as described in our previous published report D4.3 has been equipped solely with non-intrusive UQ by means of adaptive Stochastic Collocation (see figure 1). Intrusive UQ methods have not been considered due to the unrealistic implementation costs associated.
For a realistic BAC simulation, the number of parameters is very large. There are ∼16 000 energy terms in the system we are studying here, excluding the terms for all of the water molecules. These energy terms contain ∼40 000 parameters. Only limited studies have been performed to quantify uncertainties from force field parameters, using relatively simple models such as TIP4P water molecules and/or focusing on a small subset of parameters such as those for the Lennard–Jones potential or the atomic radius and charge parameters. While quantification of the uncertainties from all the force field parameters is beyond the scope of this work, we note that the above studies show that the prediction uncertainty arising from parameters may be larger than statistical simulation uncertainty. To quantify the uncertainty associated with force field parameters, more advanced sampling techniques (e.g. Active Subspaces) or in-depth implementation of intrusive methods will have to be considered.
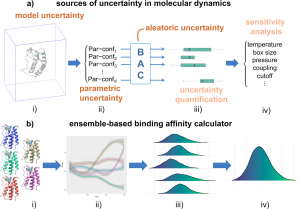
Figure 1. Sources of uncertainty and quality of predictions in molecular simulations for ensemble-based binding affinity calculations. (a) The types of uncertainties in the simulation (i) and the settings of parametric configurations (ii) are responsible for the uncertainty in predicted binding affinities (iii). Sensitivity analysis determines input parameters that most substantially impact predicted binding energy variability (iv). (b) The random errors are dealt with by ensemble approaches, in which multiple replicas (i) are simulated from initially close conformations. Neighboring trajectories in the “underlying” phase space diverge exponentially fast (ii), generating different distributions for a quantity of interest (iii). The number of replicas used to perform ensemble averaging (iv) varies, depending on the required accuracy and the power of the available computational resources.
We have a priori restricted the number of uncertain inputs, a 14-dimensional space is still too large to sample with standard SC or polynomial chaos expansions, while simple Monte Carlo is known to have a slow convergence rate. For this reason, we employ a dimension-adaptive variant of the SC sampler. The exponential increase with the number of inputs d limits practical applications of the standard SC method to less than about 10 uncertainty parameters. Non-adaptive SC for 14-parameters would have required m14 ensembles of MD simulations, with m the quadrature order.
Our UQ campaign resulted in simulating 123 ensembles of MD simulations, with quadrature required up to order 6 for the most influential parameter (e.g. temperature, see figure 2). We considered the adaptive SC method partially converged, in the sense of the relative error variance, but not the relative error mean (see figure 3). With quadrature order being refined for only a very limited number of parameters (temperature, box size and compressibility) and having exceeded our computational budget (2,000,000 CPUhs on SuperMUC-NG), we in turn limited the campaign to 10 iterations.
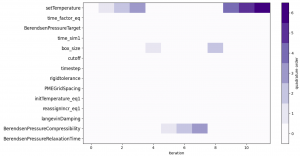
Figure 2: Refinement of quadrature order for each parameter of the BAC application with the iterations of the adaptive SC process.
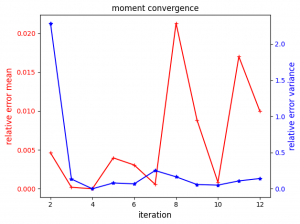
Figure 3: Evolution of the relative error mean and variance with the iterations of the adaptive SC sampling process.
The use of the toolkit [1, 2] enabled us to demonstrate that the current practice of running one or only a small number of replicas of a molecular dynamics simulation is far from sufficient to control uncertainty as we had hypothesised. Small number of replicas does not enable one to control the error in the quantities of interest, as is achieved in a statistically robust manner by ensembles. Furthermore, the toolkit enabled us to demonstrate that the distributions of properties predicted using classical molecular dynamics cannot be assumed to be Gaussian but need to be assessed in each case, particularly when long-range interactions are involved. Conversely, the findings enabled by the use of the toolkit apply to classical molecular dynamics simulation in general, including to all forms of free energy estimation made using it. In conclusion, if we wish to produce actionable results from molecular dynamics simulations, whatever the predicted quantity of interest, we must invoke ensembles for which the use of modern supercomputers is essential.
- Maxime Vassaux, Shunzhou Wan, Wouter Edeling, and Peter V. Coveney, Ensembles Are Required to Handle Aleatoric and Parametric Uncertainty in Molecular Dynamics Simulation, Journal of Chemical Theory and Computation, 2021, 17, 8, 5187–5197.
- VECMA VVUQ Toolkit: https://www.vecma-toolkit.eu/toolkit/
