For climate modelling, the range of space and time scales present in (geophysical) turbulent flow problems poses challenges, as this range is too large to be fully resolved in a numerical simulation. As such, micro-scale effects on the resolved macroscopic scales must be taken into account by empirical parametrizations (e.g. [1]). These parametrizations often involve a number of coefficients, for which the value is only known in an approximate manner. In addition, they are subject to the so-called model error or model-form uncertainty, which is the uncertainty introduced due to the assumptions made in the mathematical form of the parametrization scheme.
Within VECMA, we focus on the uncertainty in time-averaged climate statistics of geophysical flow models, due to various assumptions made in the parametrizations. EasyVVUQ allows us to assess the uncertainty in the output statistics due to the imperfectly known coefficients. In addition, we currently use EasyVVUQ for uncertainty quantification of an established local atmospheric model, DALES [2,3], which is used to simulate atmospheric processes including turbulence, convection, clouds and rain. Here, we quantify the uncertainty in model output from different sources, including uncertain physical input parameters, model choices and numerical settings, and the stochastic nature of turbulence modelling. To run the EasyVVUQ ensemble of simulations on HPC resources we use FabSim3. To address the more fundamental model-form uncertainty, we are currently investigating the use of data-driven stochastic surrogates to replace traditional deterministic parametrizations; see e.g. [5,6] for recent results.
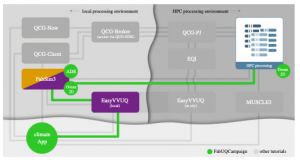
Figure 1. A Tube Mapshowing the VECMA components used in the climate application. Here ‘FabUQCampaign’ is a plugin used to run an ensemble of EasyVVUQ samples on HPC resources. Furthermore, ‘ADE’ and ‘Ocean2D’ are two example applications (advection diffusion equation and a two-dimensional ocean model) for which tutorials can be found in [4]. (Online version in colour.)
1. Gent PR, Mcwilliams JC. 1990 Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 20, 150–155. (doi:10.1175/1520-0485(1990)020<0150:IMIOCM>2.0.CO;2)
2. Heus T et al. 2010 Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES)
and overview of its applications. Geosci. Model Dev. 3, 415–444. (doi:10.5194/gmd-3-415-2010)
3. Jansson F, Edeling W, Attema J, Crommelin D. 2021 Assessing uncertainties from physical
parameters and modelling choices in an atmospheric large eddy simulation model. Phil. Trans.
R. Soc. A 379, 20200073. (doi:10.1098/rsta.2020.0073)
4. Edeling W, Groen D. 2019 FabUQCampaign. See https://github.com/wedeling/
FabUQCampaign.
5. Edeling W, Crommelin D. 2020 Reducing data-driven dynamical subgrid scale models by
physical constraints. Comput. Fluids 201, 1–11. (doi:10.1016/j.compfluid.2020.104470)
6. Crommelin D, Edeling W. 2020 Resampling with neural networks for stochastic
parameterization in multiscale systems. (http://arxiv.org/abs/2004.01457)
